 Добірка яскравих ідей ілюстрації математичної теорії учням молодшої, середньої та старшої школи у кабінетах або коридорами навчального закладу.
Добірка яскравих ідей ілюстрації математичної теорії учням молодшої, середньої та старшої школи у кабінетах або коридорами навчального закладу.
«Я – гуманітарій!» – вам також доводилось чути таку фразу від своїх учнів? Останнім часом серед підлітків та студентства стало модним заявляти, що вони є «типовими гуманітаріями». Це нібито знімає з них відповідальність та позбавляє необхідності розібратися в тому, що їм нецікаво.
Але ж ми з вами дорослі люди і прекрасно розуміємо, що інтелектуально повноцінна людина легко може опанувати будь-яку галузь знань. Питання лише в тому, щоб учню було цікаво навчатися! А ось як це зробити – тут все цілком залежить від вчителя! Можна запропонувати математичні трюки, які є справді цікавими, але їх вивчення не передбачено шкільною програмою, можна додати захоплюючу практику з залученням IT на уроках чи використовувати під час занять різноманітні ігрові прийоми тощо.
На наш погляд, найпростіший спосіб зацікавити учнів – додати до теорії яскраві наочні приклади.
Молодша школа
Для дітей молодшого шкільного віку властиве емоційне сприйняття. Тому, ймовірніше, геометричні фігури швидше запам'ятаються, якщо їх відобразити за допомогою певних звіряток чи емоційних личок.

Пам'ятаєте мультфільм про Петрика П'яточкіна? «Слоненят? – це вже цікаво!». Вчитись рахувати дійсно захопливо! Особливо, якщо треба полічити не просто певні числа, а, наприклад, яскравих звіряток!

Пригадується, як було цікаво вимальовувати літери так, ніби в них є оченята. І вчителька ще потім хвалила.
Запропонуйте учням замість звичайного знаку нерівності уявити голодного крокодильчика, що планує пообідати. Він обере те, чого більше, і відкриє ротик саме у той бік, адже він голодний!
Казковість процесу навчання захоплює школярів, тим більше в молодших класах!

Вивчаючи склад числа, кожне з них можна запропонувати уявити у вигляді будиночка, в якому жителі – окремі числа.

На годиннику всього 12 цифр, а дітлахам треба якось зрозуміти звідкіля беруться хвилини, або що означає, наприклад, час 14.07. Чому б не зробити для кабінету такі годиннички?

Опановуючи терміни «вертикаль» та «горизонталь», мабуть важкувато дібрати співзвучну асоціацію. А ось відобразити їх практичне значення досить легко!

Середня школа
Курс математики 5-8 класів ускладнюється, і далеко не завжди школярам вже зрозуміло, а яке ж практичне значення мають теоретичні відомості з цього предмету.
Деякі з ваших учнів також не одразу зрозуміли, як це пряма може бути кутом 180 градусів? Тоді пропонуємо оформити вхід до кабінету у такий спосіб:

Як швидко опанувати сенс градусів будь-якого кута
Як показує досвід, навіть ті школярі, які в молодшій школі обожнюють математику, далеко не завжди одразу розуміють сутність звичайних дробів чи зведення чисел у ступінь. Можна полегшити дитяче сприйняття у такий спосіб:

Наочні дроби
Наочне пояснення значення і співвідношення дробів
Спеціалісти стверджують: щоб швидше щось запам'ятати, потрібно його мати постійно перед очами.
Отже, табличка множення чи алгебраїчна прогресія запам'ятаються значно легше, якщо оформити відповідним чином, наприклад, шкільні сходи між поверхами.

Математичні сходинки між поверхами школи
Це один із цікавих способів відображення множення однозначних чисел – таблиця Піфагора, яку можна розмістити у кабінеті над дошкою. А поряд – табличку ділення, що наочно пояснює, як утворюються і що означають звичайні дроби.
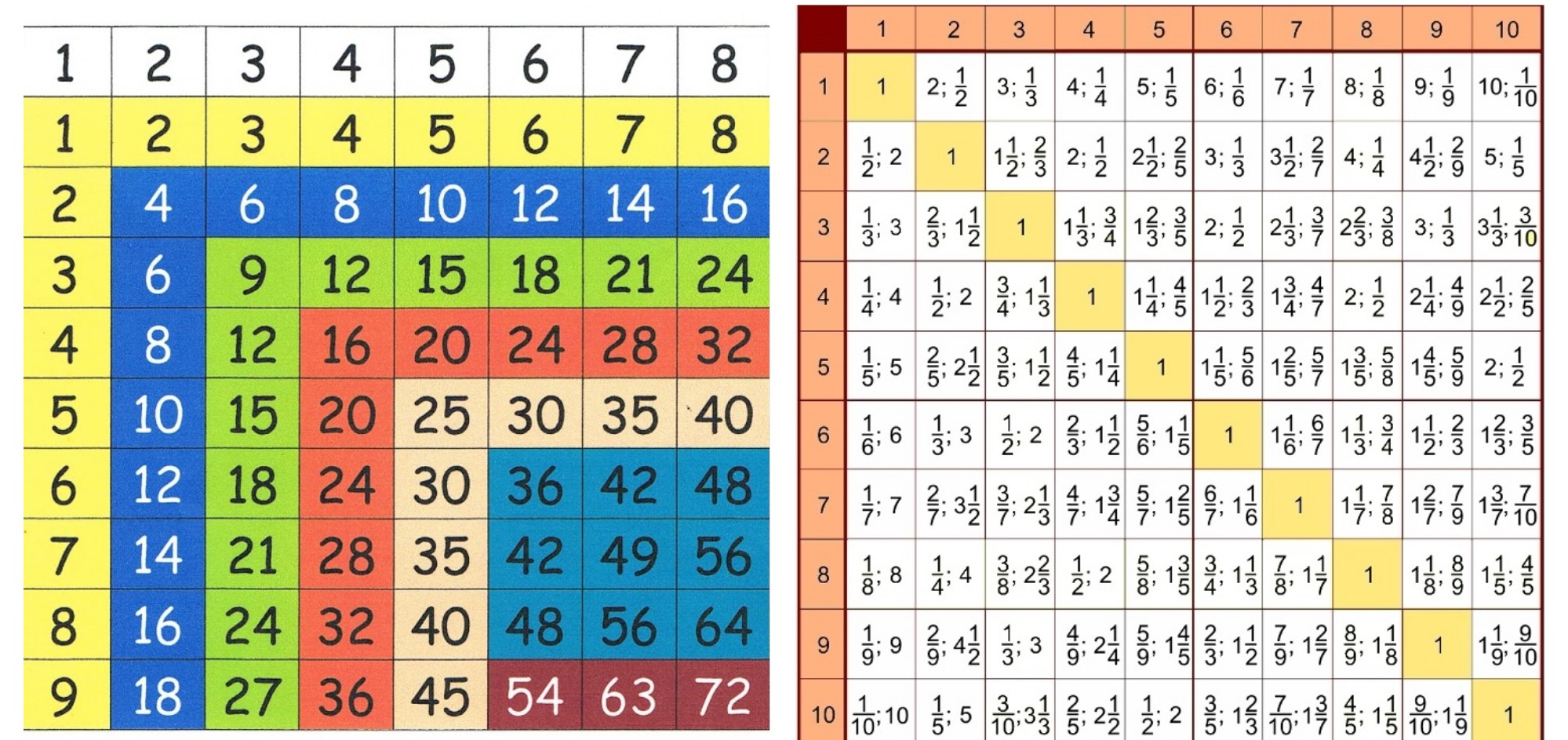
Таблиці множення та ділення для навчального кабінету
Старша школа
Коли школярі з легкістю опанують множення, у середніх або старших класах можна їх познайомити з альтернативними ментальними методами, вивчення яких не передбачено програмою.
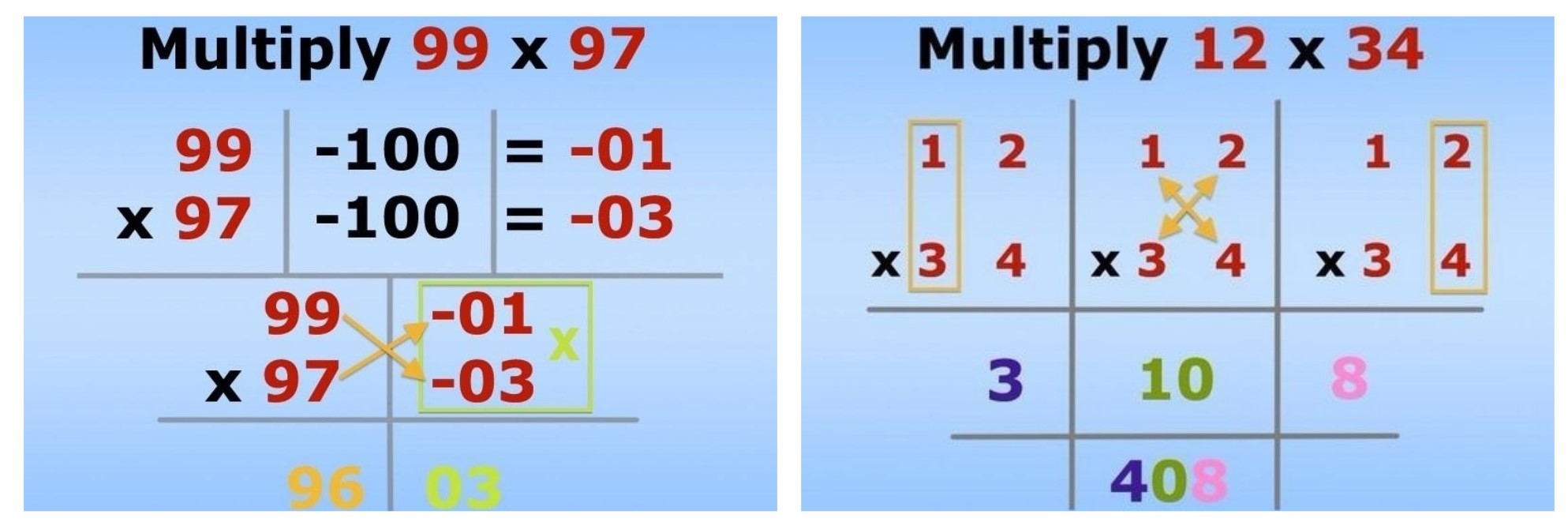
Альтернативні методи множення двозначних чисел
Вирахувати значення логарифми та знайти корені від числа можна швидше, коли сформувалось уявлення закономірністі цих обчислень. При чому спеціалісти стверджують, що графічно оформлену інформацію мозок людини сприймає швидше за числову.
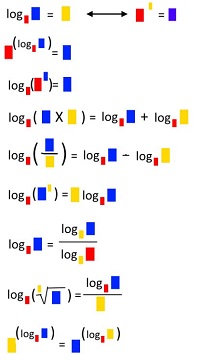
Приклади графічного зображення формул обчислення логарифмів
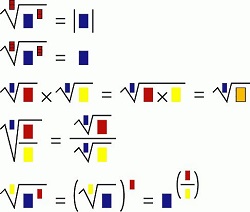
Приклади графічного зображення формул знаходження кореня від числа
В уяві більшості школярів алгебраїчні приклади так і залишаються просто числами. І якщо спитати, яке візуальне підґрунтя у такого типу алгебраїчних вправ, впевнені, меншість надасть правильну відповідь.
Запропонуйте школярам візуалізувати алгебраїчні приклади за допомогою звичайних математичних закономірностей!
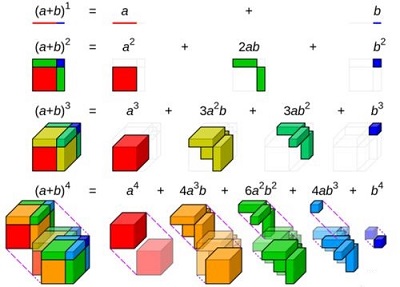
Приклад візуалізації алгебраїчних вправ
Провівши опитування знайомих, спостерігається закономірність: більшість з опитаних, цікавлячись в школі математикою, цілковито не розуміла сенс тригонометрії. Синуси, косинуси, тангенси, складні формули їх обчислення – все це так і залишилося теорією, яка незрозуміло звідкіля і для чого бралась. Може, якби пояснення тригонометричних дій супроводжувалось таким графічним відтворенням сухої теорії, зміст сприймався би жвавіше:
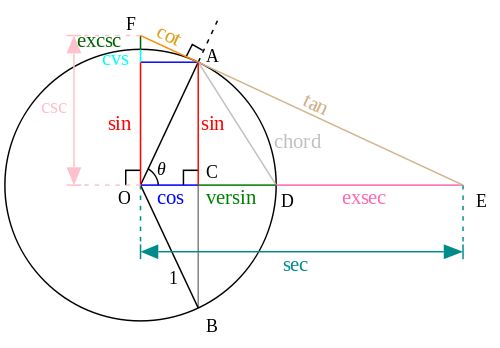
Графічний зміст основних тригонометричних понять
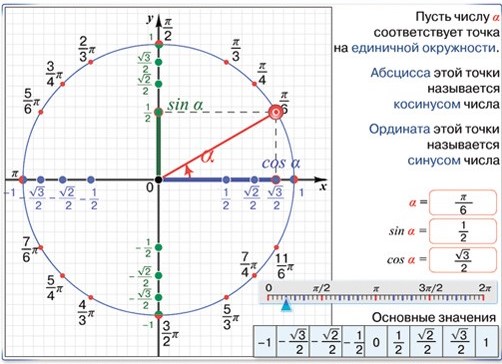
Схема обчислення синусів і косинусів
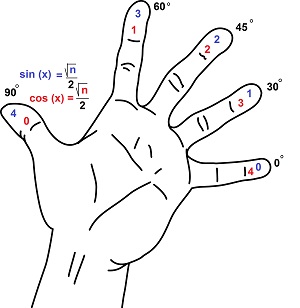
Підказка обчислення синусів та косинусів, яка завжди при собі
Графіки функцій мають математично обґрунтовану закономірність побудови. Поясніть учням сенс теорії, а для швидкого її запам’ятовування, покажіть їм веселих чоловічків, рух рук яких візуалізує графіки певних функцій.
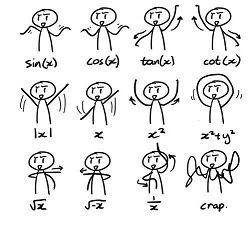
Динамічні графіки функцій
Під час практичних занять в якості творчого, запропонуйте учням завдання, на кшталт:
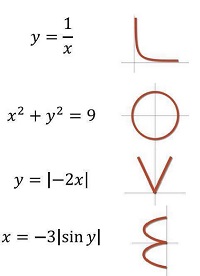
Звісно, навчання в школі – це двостороння взаємодія між учителем і учнем. Тому успіх залежить від докладених зусиль обома сторонами! А ось чи буде учень сприймати математику, як суху теорію чи справді закохається у предмет і запам'ятає уроки на все життя – цілковито залежить від вчителя!

Немає коментарів:
Дописати коментар